一,熵的来源
熵首次出现是在物理学中,描述热力系统的无序情况;后来信息论也同样用熵来描述不确定事件!
打个比方,8支篮球队,争夺1个冠军,哪个队伍是冠军,这就是不确定事件!
如果每支队伍夺冠概率一样,那么只需猜测3次就能猜到冠军是谁,利用二分法,第一次猜1到4支队伍中,如果猜对了,接着第二次猜1到2队伍中,又猜对了,则第三次猜1队伍
所以在等概率情况下,哪个队伍是冠军这个不确定事件的熵就是3
二,熵的定义
下面来看看熵在有限离散样本下的求值公式
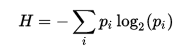
其中 P 是 i 的概率函数
重新计算篮球赛谁夺冠军的不确定事件的熵
因为是每支队伍都是等概率夺冠,所以 P = 1/8 ,然后底数为 2 的对数值为 -3,一共有 8 支队伍,所以 H = -8 * 1/8 * ( -3 ) = 3
这里是采取比较通俗易懂的方式来讲解熵的含义,而且是等概率的情况,如果每支队伍夺冠概率不一样就变成
H = – (p1*log(p1) + p2*log(p2) + … + p8*log(p8))
当概率相同时,夺冠事件是最不确定的,所以熵 H 也是最大的
三,相对熵
下面来分析下两支队伍在夺冠这事件上的熵含义
1 队伍有可能夺冠,2 队伍也有可能夺冠,这两支队伍夺冠的两件不确定事件,怎么描述他们之间的关系呢?
首先来看看相对熵的定义
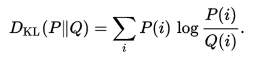
1 队伍在一场比赛获胜概率函数是 P,2 队伍在一场比赛获胜概率函数是 Q,i 表示第几场比赛
相对熵又称为KL散度,KL距离,是两个随机分布间距离的度量,将定义公式化简如下
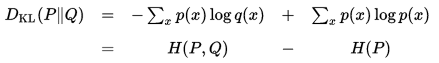
可知道,当Hp(q)=H(p)时,KL距离为零,即p(x)=q(x)时,H(P,Q) = H(P,P) =H(P),相对熵为零
物理意义就是,1 和 2 队伍每场比赛获胜的概率都一样,所以他们最终夺冠这件事的不确定性一样,即两者的熵相等,两者的相对熵为零
四,交叉熵
定义交叉熵为
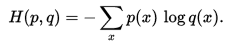
用相对熵转换一下
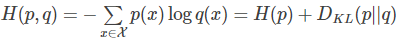
根据相对熵特性可知,当p(x)=q(x)时,相对熵为零,这时候交叉熵为极值
五,交叉熵的应用
交叉熵极值条件特别合适用来描述两个随机分布的相似性
在深度学习中,采用交叉熵作为损失函数,来描述模型输出和真实取值之间的相似性
p:真实样本分布,服从参数为p的0-1分布,即p(0) = y, p(1) = 1 – y;
q:待估计的模型,服从参数为q的0-1分布,即q(0) = y^, q(1) = 1 – y^;
两者的交叉熵为:
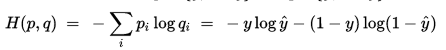
当有多个样本时,求整体样本损失情况,采用均值即可
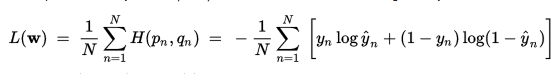
Leave a Reply