简单地说:描述变化趋势
比如一条曲线,当x移动时,y变化的趋势,有时候y增长,有时候变小,导数就是描述这种变大变小的趋势
举个例子,最简单的 y=2x 函数,当x从0到1移动时,y也从0到2变化,y的变化是x变化的2倍,这个函数的导数就是2
看看图片感受y随着x的变化,横坐标是x,纵坐标是y
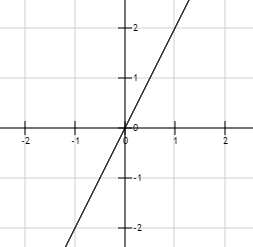
导数的值是如何确定的呢?来看看导数的公式定义
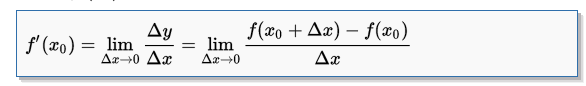
导数的物理图像
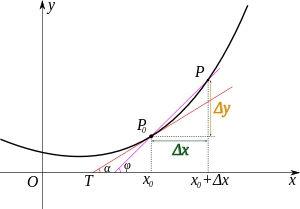
根据公式求 y = 2x 的导数:
△y=2(x0+△x)-2(x0) =2△x,再除以△x,就等于2,而且跟x0没有关系,即不管x在取什么值,函数的导数都为2
这里的导数这么简单求得,是因为函数变化趋势很简单,就是x变化的2倍就是y的变化了
对于复杂点的函数,比如 y=x^2,
△y=(x0+△x)^2-x0^2 =x0^2+2×0△x+△x^2-x0^2=2×0△x+△x^2,再除以△x,就等于2×0+△x,当△x趋于0时,最终求得导数 2×0
这时候的导数是跟x取值有关的,即不同x0,有不同的导数,如下图所示
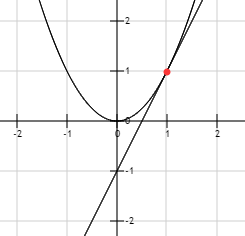
当x=1时,函数的导数为 2 ,也就是直线y=2x在点x=1的y值
当x=0时,导数为0时,表明y不再变化了,达到极值,这时候y值确实函数y=x^2的最小值
这是理想情况下局部极值,并不是全局的,有些函数是多个导数为0的极值点,比如下图
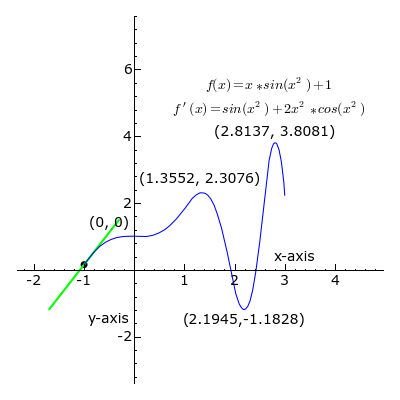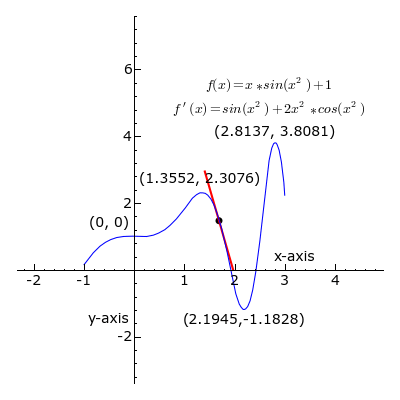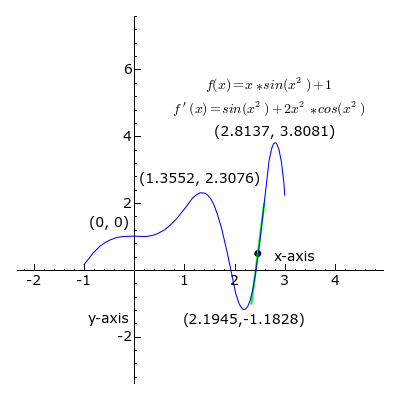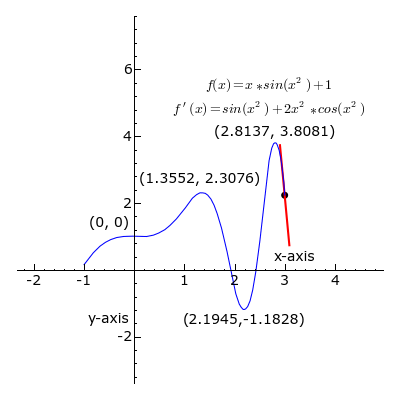
更多导数和求导公式的资料,请参考这里
Leave a Reply